Bauschinger Effect in High-Strength Low-Strain-Hardening Materials - Post [1/2]
페이지 정보
작성일posted onLink
본문
Bauschinger
Effect in High-Strength Low-Strain-Hardening Materials - Post [1/2]
In a series of 2 posts starting this week, the Bauschinger effect in high strength low-strain-hardening materials will be discussed.
1. Introduction
It is noteworthy that cold-forged, high-strength materials or parts can often bypass heat treatment after being formed, which minimizes the amount of post-work due to twisting or bending [1]. Detailed investigation of the material to be forged, die structure, forming process, and material conditions should precede cold forging of a high-strength material, since the process is subject to extreme working conditions caused by high die pressure.
Optimization
of process design and die structure can be achieved using metal forming
simulation technology. From an application perspective, the first thing process
design engineers should do is optimize the process and die designs. Second,
they should determine the optimized state of the material, since it can easily
be realized. Finally, they should select the optimized die material, and
continue to encourage and assist die material engineers in developing proper
die materials for cold metal forming of high-strength materials.
It
should also be noted that a material used for multi-stage automatic cold
forging is usually drawn prior to being forged. The drawing process relies
basically on plastic deformation under tension, and the drawn material is thus
subject to the Bauschinger effect [2-5] in the subsequent forging processes,
where plastic deformation usually occurs in the compression state of stress.
The Bauschinger effect accompanies a change in the characteristics of the
stress–strain relationship of a material due to its micro structural stress
distribution. This behavior causes the compression strength of the drawn
material to decrease and is one of the general characteristics of poly crystalline metals.
Even though the Bauschinger effect occurs in materials with
high strain-hardening capability, its influence on the forming load is
relatively weak, because the strain-hardening effect surpasses the Bauschinger
effect. For this reason, application of the Bauschinger effect has been
neglected by researchers.
Recently, there have been numerous attempts to use high-strength materials to meet the demand for decreased weight and higher reliability in automobiles, as well as to reduce costs and protect the environment. In this case, it is essential to minimize the forming load. Hence, it is of great importance to take advantage of the Bauschinger effect in the cold forging of high-strength materials. It is natural to utilize the Bauschinger effect in multi-stage automatic cold forging, since the initial material is often drawn in a tensile state of stress before being extruded or headed in a compression state of stress.
In this study, cylinder compression tests are conducted for
drawn rods made of very different materials (ESW105 [1]), and their Bauschinger
effects are quantitatively demonstrated. Note that ESW105 is characterized by
its high strength and low strain-hardening capability.
2. Preparation of the specimens and analysis of the drawing process
The material tested in this research was ESW105 which has a
very weak strain-hardening capability with high yield strength [1, 6]. Note
that ESW105 is a special steel fabricated by pre-heat treating a commercial
steel, and has been applied successfully to many automobile parts, including
tie-rods, bolts, etc. [1]. Also note that cold-forged ESW105 products can
bypass post-heat treatment, since the initial materials are pre-heat treated.
Pre-heat treating is both environmentally friendly and cost-effective compared
with post-heat treating, since it minimizes the amount of post-work (including
straightening and the like). The base material for the ESW105 used in this
study was AISI51B20. It is important to emphasize that the AISI51B20 base
material was especially pre-heat treated to fabricate the high-strength ESW105
material with very low strain-hardening capability.
The experimental procedure was composed of two steps. The
first step was to fabricate the test rods, which were drawn by 10, 20, 30, 40,
and 50% reductions in area from the initial pre-heat-treated steel coil. Figure
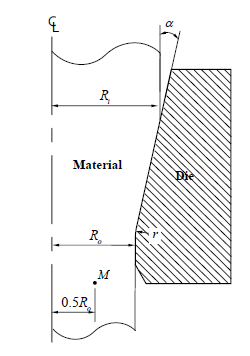
1 shows a schematic diagram of the drawing process employed to fabricate the
drawn rods. In the drawing process design, Ri = 8.25 mm, r = 5.0 mm, and α =12.0°
were fixed, while the exit radius varied from 7.829 to 5.835 mm to give the
various reductions in area. The steel coil was well lubricated with phosphates
prior to being drawn. The cylindrical specimens to be compressed were prepared
according to ASTM E9 from the drawn rods, and their heights and radii were all
15.0 and 5.0 mm, respectively.
Figure
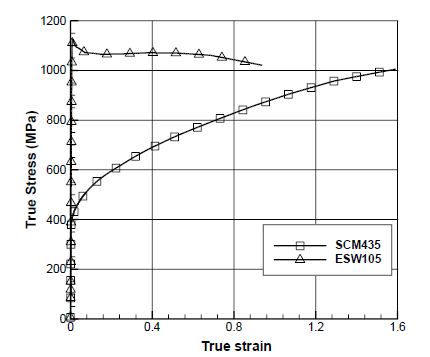
2: Flow stress curves
First, we carried out a finite element simulation [7] of the test drawing process to investigate the strain distribution (i.e., the initial state) of each specimen. The flow stresses of ESW105 employed in this simulation, and shown in Fig. 2, were obtained via the material identification algorithm based on tensile tests [8]. In the figure, SCM435 exhibited typical strain-hardening behavior, while ESW105 showed a negligible strain hardening capability. Since the friction is relatively low during the drawing process, the frictional coefficient was assumed to be 0.03.
The predicted effective strains associated with the five
reductions in area are shown in Fig. 3. In this study, the mean effective
strains were calculated from the effective strains at the half radii of the
drawn rods (note the point marked M in Fig. 1). When the mean effective strains
are compared with the ideal effective strains calculated from the logarithmic
values of the reductions in area during the drawing process, they were slightly
greater than the logarithmic strains, reflecting the shear deformation
experienced while drawing.
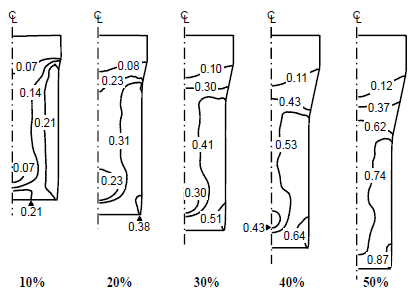
Figure 3: Effective strain for the test drawing process ESW
105
Further discussions about cylinder compression tests and the conclusion of this research work will be published in the next article.
Authors:
M. S. Joun, School of Mechanical Engineering/Engineering Research Institute, Gyeongsang National University
S. T. Ahn, Samhwa steel, Korea
H.T. Jin, Dept. of Mechanical Engineering, Gyeongsang National University, Korea
Y. H. Son, Youngsin Metal Industrial Co., Korea
D. J. Yoon, Korea Institute of Industrial Technology, Incheon, Korea.
Publication:
Proceedings of the 13th Asian Symposium on Precision
Forging (ASPF2015) Gyeongju, Korea, September 17-18, 2015
References:
[1] S. S. Han, J. G. Eom, S. T. Ahn, S. M. Jang, Y. H. Son,
K. Kim, D. J. Yoon, M. S. Joun, 2010, Plastic deformation behavior of
pre-heat-treated high-strength steel for application in forging, Steel Research
International, Vol. 81, pp. 250-253.
[2] G. Cailletaud, 1992, A micromechanical approach to
inelastic behavior of metals, International Journal of Plasticity, Vol. 8,
pp.55-73.
[3] M. Choteau, P. Quaegebeur, S. Degallaix, 2005,
Modelling of Bauschinger effect by various constitutive relations derived from
thermodynamical formulation, Mechanics of Material, Vol. 37, pp.1143-1152.
[4] X. Lemoine, A Aouafi, 2008, Bauschinger effect
correspondence of experimental test, International Journal of Material Forming,
Vol. 1, pp.241-244.
[5] M. A. Vicente Alvarez, M. Bergant, T. Perez, 2010,
Relaxation of the bauschinger effect by thermal treatment on tempered
martensitic steels, Material Science and Enineering A, Vol. 527, pp.5939-5946.
[6] M.S. Joun, J.G. Eom, M.C. Lee, J.H. Park, D.J. Yoon,
2008, Tensile test based material identification program AFDEX/MAT and its
application to two new pre-heat treated steels and a conventional Cr-Mo steel,
International Journal of Modern Physics (IJMPB), Vol. 22, No. 31-32, pp.
5774-5779
[7] M. S. Joun, M. C. Lee, J. G. Eom, 2011, Intelligent
metal-forming simulation, Y. L. Yao, M. Bement, Z. C. Xia, B. Kinsey, X. Yang
(Eds.), ASME Conference Proceeding, Corvallis, Oregon, pp.161 - 168.
[8] M. S. Joun, J. G. Eom, M. C. Lee, 2007, A new method for acquiring true stress-strain curves over a large range of strains using a tensile test and finite element method, Mechanics of Material, Vol. 40, pp.586-593.

