Comparison of rigid-plastic and elasto-plastic finite element predictions of a tensile test of cylindrical specimens – Post 1
페이지 정보
작성일posted onLink
본문
Comparison of rigid-plastic and elasto-plastic finite element predictions of a tensile test of cylindrical specimens - Post 1
Tensile test gives valuable information about finite element analysis and some criterion on its evaluation. It should be noted that tensile test can be not only used for acquisition of flow stress but it can be also useful for evaluating accuracy of finite element simulation of metal forming processes because it is mechanically very simple, i.e., its boundary conditions are clear. Many researchers have thus studied material identification, based on the tensile test of cylindrical specimens [1-6]. However, very few researchers have simulated the tensile test with higher accuracy [6].
Joun et al. [6] developed an iterative
approach for acquiring flow stress of material at the room temperature using
tensile test of cylindrical specimens and its finite element prediction by
rigid-plastic finite element method. This approach has a merit that flow stress
at large strain can be obtained and it can be used to predict tensile test with
higher accuracy by rigid-plastic finite element method. However, due to the
limitation of the theory of rigid-plasticity, the approach may be exposed to some errors at the elastic region.
Rigid-plastic
finite element method inherently approximates a plastic deformation of material
in the elastic region and thus its accuracy depends more or less on the
process. Elastoplastic finite element solutions are also dependent on the
specific theory and numerical schemes. Both rigid-plastic and elastoplastic
finite element methods have their own strengths and drawbacks and thus it is
meaningful to reveal the similarity and difference between the two approaches in
a quantitative manner. However, it is not easy to find the related research
work.
In
this series of posts, a tensile test of SCM435 is simulated by both
rigid-plastic and elastoplastic finite element methods and their predictions
are compared to clarify the difference and similarity. In the simulation, the
same flow stress which was obtained by the iterative approach to identifying
material property using tensile test of cylindrical specimen [7].
Rigid-plastic
finite element analysis of tensile test of cylindrical specimen
A
coil material of SCM435, spheroidized with annealing, is used for this study.
Initial yield strength of the material obtained by tensile test shown in Figure
1 is 385 MPa. The tensile test was studied by both a rigid-plastic finite
element method [8,9] and an elastoplastic finite element method [10]. In the
rigid-plastic finite element method, a traditional isoparametric quadrilateral
linear element with reduced integration scheme was employed. The same mesh
system was employed for the elastoplastic finite element method together with
B-bar element technique [11] considering numerical locking phenomena occurring
in simulating incompressible material and computational efficiency. The
material was assumed isotropic and to obey Huber-von Mises yield criterion.
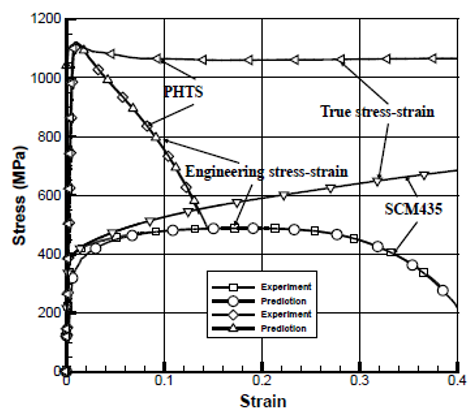
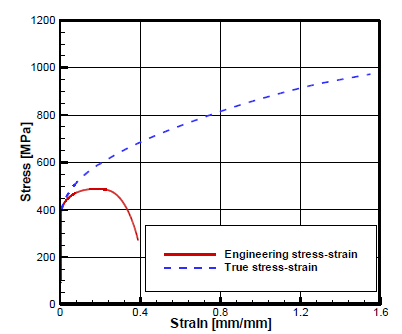
Figure 2:
Engineering stress-strain curve and its associated true stress-strain curve
obtained by a tensile test of SCM435 cylindrical specimen
Figure
3(a) shows the predicted history of deformation of the tensile test, which were
obtained
using
the flow stress in Figure 1 and rigid-plastic finite element method. This
simulation was accomplished by 1000 solution steps which are sufficiently small
enough to neglect the numerical effect.
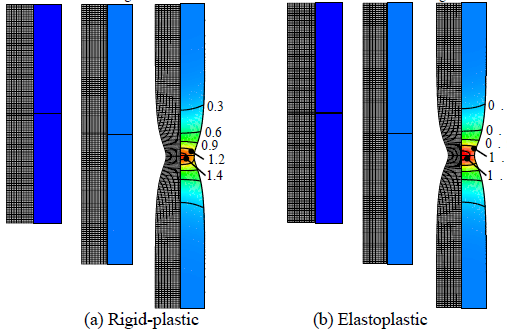
Figure 3: Predicted
equivalent strain deformation history for the tensile test of SC435
In
the next week’s post, the elastoplastic predictions will be discussed in detail
and the comparison would be made.
References:
[1]
Bridgman P.W.:Studies in large flow and fracture, McGraw-Hill, New-York, 1952.
[2]
ZhangK.S.:Fracture prediction and necking analysis,Eng.Fract.Mech.52 (1995)
575-582.
[3]
Komori K.:Simulation of tensiletest by node separation
method,J.Mater.Process.Technol.125-126 (2002) 608-612.
[4]
MironeG.:A new model for the elastoplastic characterization and the
stress-strain determination on the necking section of a tensile specimen,Int.
J.Solids.Struct.41 (2004)3545-3564.
[5]
Springmann M., KunaM.: Identification of material parameters of the
Gurson-Tvergaard-Needleman model by combined experimental and numerical
techniques,Computational Materials Science 32 (2005) 544-552.
[6]
M. S. Joun, J. G. Eom, M. C. Lee:A new method for acquiring true stress-strain
curves over a large range of strains using a tensile test and finite element
method, Mechanics of Material40(2008) 586-593.
[7] J. G. Eom, Y. H. Son, S. W. Jeong, S. T. Ahn, S. M. Jang, D. J. Yoon, M. S. Joun:Effect of strain hardening capability on plastic deformation behaviors of material during metal forming, Material and Design 54(2014)1010-1018.
[8]
C. H. Lee, S. Kobayashi: New Solutions to Rigid-Plastic Deformation Problems
Using a Matrix Method, J. Eng. Ind. 95 (1973) 865-873.
[9]
M. C. Lee, S. H. Chung, S. M. Jang ans M. S. Joun: Three-dimensional simulation
of forging using hexahedral and tetrahedral elements, Finite. Elem. Anal. Des.,
45 (2009) 745–754.
[10]
W. J. Chung, M. S. Joun:Elastoplastic module of AFDEX 2D, Proc. of 2013 KSTP
AutumnConference(2013)57-60.
[11]
J. R. Hughes:The Finite Element Method:Linear Static and Dynamic Finite Element
Analysis,Prentice-Hall, New Jersey, 1987.

